Roulette Systems: 5 Dollar Harley 🏍️
| Air Date: |
| System Type: | Positive Progression |
|---|---|---|---|
| Buy-in: |
 $100
$100 |
Bet per Spin: |
 $5
$5 $10
$10 $20
$20 $500
$500 |
| Total Bets: | $245 | Total Win/Loss: | -$45 |
| Total Expected Loss: | -$12.88 | Total Comp Value: | $2.57 |
| Total Spins: | 29 | Seconds between Spins: | 22 |
| Rating: | JackAce Rating: |
Betting Schemes
Tier 1 ($5) | Tier 2 ($10) | Tier 3 ($20) | Tier 4 ($500)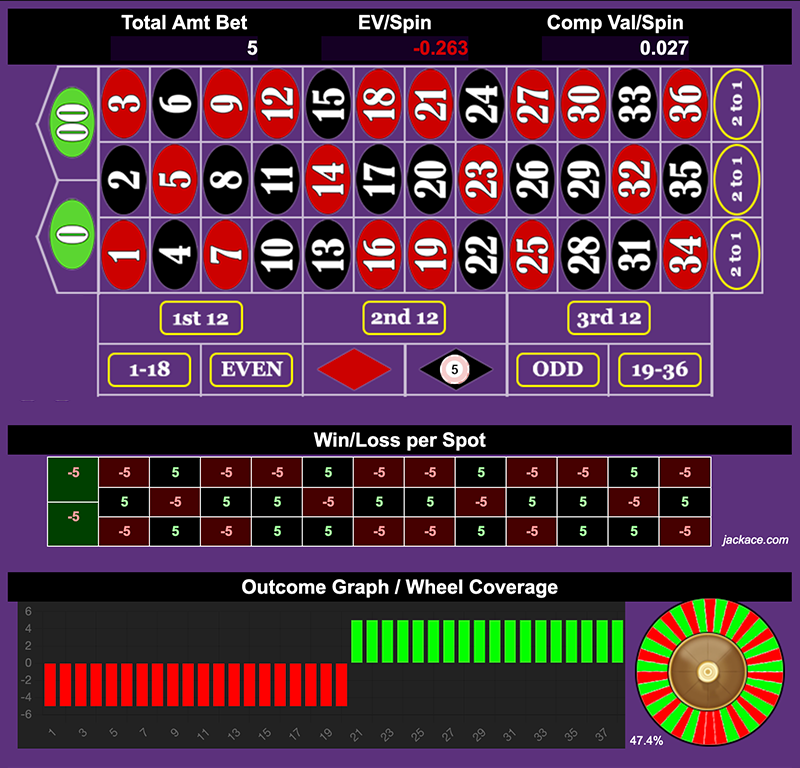
View this bet in the Roulette Bet Analyzer
| Spin # | Number | Result | Amount Bet | Running Total | Time | Notes |
|---|---|---|---|---|---|---|
| 1 |

|
-$5 WHACK |
$5 | -$5 | 2:22 | |
| 2 |

|
-$5 WHACK |
$5 | -$10 | 2:46 | |
| 3 |

|
+$5 | $5 | -$5 | 3:06 | |
| 4 |

|
-$10 WHACK |
$10 | -$15 | 3:33 | |
| 5 |

|
+$5 | $5 | -$10 | 3:51 | |
| 6 |

|
-$10 WHACK |
$10 | -$20 | 4:17 | |
| 7 |

|
-$5 WHACK |
$5 | -$25 | 4:50 | |
| 8 |

|
-$5 WHACK |
$5 | -$30 | 5:15 | |
| 9 |

|
-$5 WHACK |
$5 | -$35 | 5:38 | |
| 10 |

|
+$5 | $5 | -$30 | 6:08 | |
| 11 |

|
-$10 WHACK |
$10 | -$40 | 6:41 | |
| 12 |

|
-$5 WHACK |
$5 | -$45 | 7:12 | |
| 13 |

|
+$5 | $5 | -$40 | 7:43 | |
| 14 |

|
+$20 | $10 | -$20 | 8:09 | |
| 15 |

|
-$20 WHACK |
$20 | -$40 | 8:34 | Alex put the $20 on 0. |
| 16 |

|
-$5 WHACK |
$5 | -$45 | 9:04 | |
| 17 |

|
-$5 WHACK |
$5 | -$50 | 9:22 | |
| 18 |

|
+$5 | $5 | -$45 | 9:46 | |
| 19 |

|
+$20 | $10 | -$25 | 10:04 | |
| 20 |

|
-$20 WHACK |
$20 | -$45 | 10:35 | |
| 21 |

|
+$5 | $5 | -$40 | 10:50 | |
| 22 |

|
-$10 WHACK |
$10 | -$50 | 11:13 | |
| 23 |

|
+$5 | $5 | -$45 | 11:23 | |
| 24 |

|
+$20 | $10 | -$25 | 11:45 | |
| 25 |

|
-$20 WHACK |
$20 | -$45 | 12:11 | |
| 26 |

|
+$5 | $5 | -$40 | 12:23 | |
| 27 |

|
+$20 | $10 | -$20 | 12:43 | |
| 28 |

|
-$20 WHACK |
$20 | -$40 | 12:54 | |
| 29 |

|
-$5 WHACK |
$5 | -$45 | 13:17 | |
|
Expected Loss |
Total Bets |
Total Win/Loss |
||||
| -$12.88 | $245 | -$45 |
Progressive system where you get 2 small wins and then $20 Straight-up followed up by a $500 Straight-up.
I like this system, but I think step 3 should be a little easier to hit (like a single Street?), before you go for the Jugular.
In CEG's review, Alex asked me to calculate the probability of hitting the $500 jackpot. Here's the calculation:
\begin{align} \\ \frac{18}{38} \times \frac{12}{38} \times \frac{1}{38} \times \frac{1}{38} &= \frac{216}{2085136} \\ \\ &= 0.00010359... \\ \\ &\approx \frac{1}{9653} \\ \\ \end{align}
This means for every time we start with the $5 bet, we will be successful in winning the next 4 bets in a row about once every 9,653 attempts. Any loss will reset the attempt. But keep in mind that it's possible to "win bullets" along the way.
Running this system through my simulator, I got the following stats:
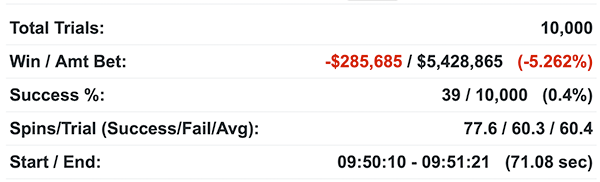
Out of 10,000 trials, we hit the goal of "winning the Harley" a total of 39 times. The other 9,961 times, we lost the $100.
This seems about right. If only used 20 bullets per buy-in, we'd expect to be successful around 20 or 21 times. But since it's possible to "win bullets" on the 2nd and 3rd tiers, that bumps that number up by almost double.